Sound

Sound waves are produced by and carried by the vibrations of particles. These vibrations travel through the medium into our ears and cause the eardrum to vibrate. These vibrations are converted into electrical signals which are carried along the auditory nerve to our brain as auditory signals where they are then interpreted.

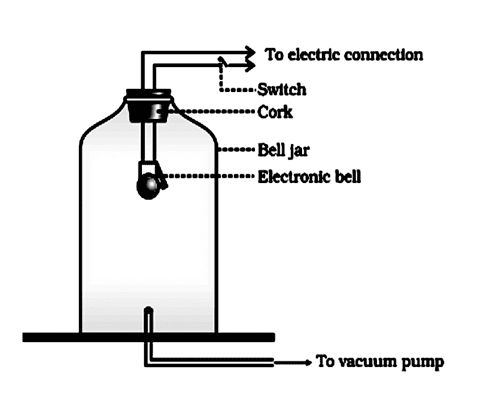
Sound waves can travel through solids, liquids and gases as these all contain particles. Sound waves rely on the vibrations being passed along through the particles. In a vacuum there are no particles so sound waves are unable to travel through a vacuum. This explains why sound cannot be heard in space.

A common experiment which proves this uses a bell jar with a vacuum pump attached. When the vacuum pump is not switched on, the ringing of the electronic bell can be heard. This is because the sound waves are passed along using the vibrations of the particles in the air and glass.

When the vacuum pump is switched on, the air particles are all sucked out of the jar to create a vacuum. The sound waves can no longer travel as there are no particles to vibrate and the sound of the bell can no longer be heard, although we can observe it ringing.

The speed of sound in air is approximately 340 m/s, though this may vary depending on the temperature and pressure. The speed of sound in a liquid is a lot higher. This is because the particles in a liquid are closer together, meaning that the vibrations can be passed between the particles much quicker. The speed of sound through solids is even faster as the particles are even closer to one another and can pass the vibrations on very quickly.

Sound waves are longitudinal waves which, like all other waves, can be reflected and refracted. When the sound waves hit a surface, they are reflected. The law of reflection also applies to the reflection of sound waves where the angle of incidence is equal to the angle of reflection. Reflected sound waves are known as echoes.

Measuring the speed of sound

Echoes can be used to measure the speed of sound waves through air. If you stand 50 m away from a wall and clap your hands or bang two pieces of wood together, you should be able to hear an echo.

You can record the time taken for you to clap 40 times. The distance travelled was 100 m per clap (to the wall and back again), and there were 40 claps. The total distance is therefore 100 x 40 = 4,000 metres. The speed of sound can then be calculated using the equation:

You can also use a resonance tube and tuning forks to measure the speed of sound. A resonance tube is made of plastic and is filled with water. The height of the water in the tube can be adjusted as the sound waves will reflect off the surface of the water. A sound is made by striking the open end of the tube with a tuning fork. The water in the column is adjusted until the loudest sound can be heard. The first resonance will be heard when the length of the air in the tube is equal to a quarter of the wavelength. You can check the result by lowering the water level to find the next resonance at 3/4 of the wavelength. The speed of sound is then found using the formula v = f x λ. Where  is the wave speed in metres per second, f is the frequency in hertz and λ (lambda) is the wavelength in metres.

Pitch, frequency and amplitude

Frequency is a measure of the number of vibrations of the source every second and it is measured using the unit hertz (Hz). If a source has created a frequency of 60 Hz, this simply means that it has vibrated 60 times every second. Pitch is a term used to describe how high or low a sound is.

The frequency of vibrations of the source is related to the pitch of the sound made by the same source. If the frequency is high, there are many vibrations and the sound is high pitched. If the frequency is low, there are fewer vibrations and the sound is low pitched. Smaller objects when struck tend to produce sound waves at a higher frequency and of a higher pitch. Similarly, larger objects when struck tend to produce sound waves at a lower frequency and of a lower pitch.

Sound waves can be observed and displayed using a microphone and a device called a Cathode Ray Oscilloscope (CRO) or oscilloscope for short. The microphone converts sound energy into electrical energy in the form of electronic signals. The oscilloscope is then used to display these electronic signals as a pattern of waves.

The waves seen on the oscilloscope provide information about the volume, as well as the frequency and therefore pitch of the sound.  Amplitude is a measure of the strength of vibration of the source. Sound waves travel through vibrations. The bigger the vibrations the more sound is created and the louder the sound becomes. The amplitude of the wave seen on the oscilloscope is the distance between the resting position and the peak of the wave. The higher the amplitude, the stronger the vibrations of the source are and the louder the sound becomes. A small amplitude shows that the vibrations of the source have been less powerful and the sound is quieter.

The number of waves and distance between them provides information about the frequency of the sound and therefore the pitch. The closer the waves are to each other, the higher the frequency and the higher the pitch of the sound.

A lower pitched sound will have fewer completed waves per second, so fewer complete waves will be seen on the oscilloscope. Any changes to the volume or pitch of the sound can be observed through changes to the amplitude and frequency of the wave patterns seen on the oscilloscope screen.

The diagrams below show typical oscilloscope traces for a low-pitched and a high-pitched sound:

Audible range

The frequency range for human hearing is 20–20,000 Hz. This is known as the audible range or hearing range. Any sounds with a frequency which is outside of this range will not be heard by humans. This range changes with age. As you get older, you become less able to hear sounds at higher frequencies.

Some objects may vibrate at frequencies higher than 20,000 Hz and thus create high frequency vibrations which are beyond the range of human hearing. These sounds are known as ultrasound waves. Ultrasound can be used in medical diagnosis to look at soft tissues inside the body or viewing the unborn foetus. Some vibrations occur at frequencies below 20 Hz and these are known as infrasound and cannot be heard by human beings.

The Doppler effect

In the previous example using the ripple tank, the source of the waves was static and in the same position.  We know that wave speed is related to frequency and wavelength through the equation:

As long as the wave speed remains constant, the observed frequency and wavelengths of the waves produced does not change. Assuming that the wave speed remains constant, an increase in frequency results in an increase in wavelength, and a decrease in frequency results in a decrease in wavelength.

However, when the source of the waves is moving relative to the observer, the observed frequency and wavelength do change. For example, imagine two people are stood 100 metres apart. Directly in between them at a distance of 50m from both people is a radio emitting sound waves at a speed of 0.3 m/s.

As the distance between each person and the generator is 50 m, and all of the waves are travelling at the same speed, the frequency of the sound heard by both people would be the same. If it took 1.5 seconds for each person to hear the sounds, the frequency would be calculated as:

A change to the distance between each person and the radio results in a change in the frequency of the sound heard by each person. Imagine that the radio was moved 25 m closer to Person A. The distance between the radio and Person A is 25 m and the distance between Person B and the radio is 75 m. As Person B is now further away from the source of the sound, Person A would hear the sound before Person B. Let’s imagine that Person A heard the sound in 1 second but it took 2 seconds for Person B to hear the sound.

The frequency of the sound heard by Person A is calculated as:

The frequency of the sound heard by Person B is calculated as:

The frequency of the sound heard by Person A would appear to the observer to be higher than the frequency of the sound heard by Person B.

As the sound has moved towards Person A they have observed the frequency to increase. As the sound has moved away from Person B they have observed the frequency to decrease.

This difference in frequency observed by Persons A and B means that there is also a difference in the wavelengths observed.

Assuming that the speed of the sound waves remains constant at 0.3 m/s, the wavelength of the waves observed by Person A would be calculated as:

Assuming that the speed of the sound waves remains constant at 0.3 m/s, the wavelength of the waves observed by Person B would be calculated as:

The actual frequency of the sound emitted by the source has not altered but there is a change to the observed frequency and wavelength of the wave due to the movement of the source relative to the observers. This is known as the Doppler effect and is commonly noticed by people as the change in sound when they hear the changes in the sounds of the siren as an emergency vehicle such as police car goes past. As the police car approaches you the siren may sound very high pitched, meaning that it has a high frequency. As the car moves past you and travels away, the sound of the siren becomes lower in pitch and therefore lower in frequency. Sirens are designed like this so that you can tell when they are approaching and from which direction they are moving.