Using factorisation

Another way in which we can simplify fractions and equations is to factorise the different parts to find common terms. At first sight, a fraction may look to have very complicated parts but this does not mean that our calculations have to be. By factorising the numerators and denominators we may find obvious common terms on the top and bottom which can be cancelled.

Example

Simplify the following fraction:

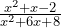
At first this looks to be very hard as we have no obvious common terms on the top and bottom of the fraction. However, if we factorise the top and bottom separately we will see that it is not so difficult:

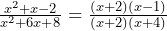
Now we can see that we have a common term on the top and bottom of  which can be cancelled to leave us with:

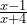
This same technique of factorising the numerator and denominator to identify potential common terms which can be eliminated can always be used. By cancelling any common terms, the fraction that we have will be simpler to work with.

Example

Simplify

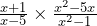
By factorising the second fraction and then bringing all the terms on the top and bottom together in the multiplication we find that this equation is the same as:

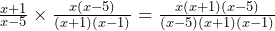
Now the brackets that appear on both the top and bottom of the fraction can be cancelled. These are  and  which leaves us with:

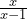
Clearly, this is much simpler than the equation that we originally had and can be left in this form as we cannot simplify any further.

The exact same method of factorising the numerator and denominator of each fraction to find common terms can be used even when the calculation requires a division. The only difference is the obvious one of changing the divide to a multiply whilst flipping the second fraction. Once this is done we can go ahead and factorise the fractions and cancel common terms.