In this post
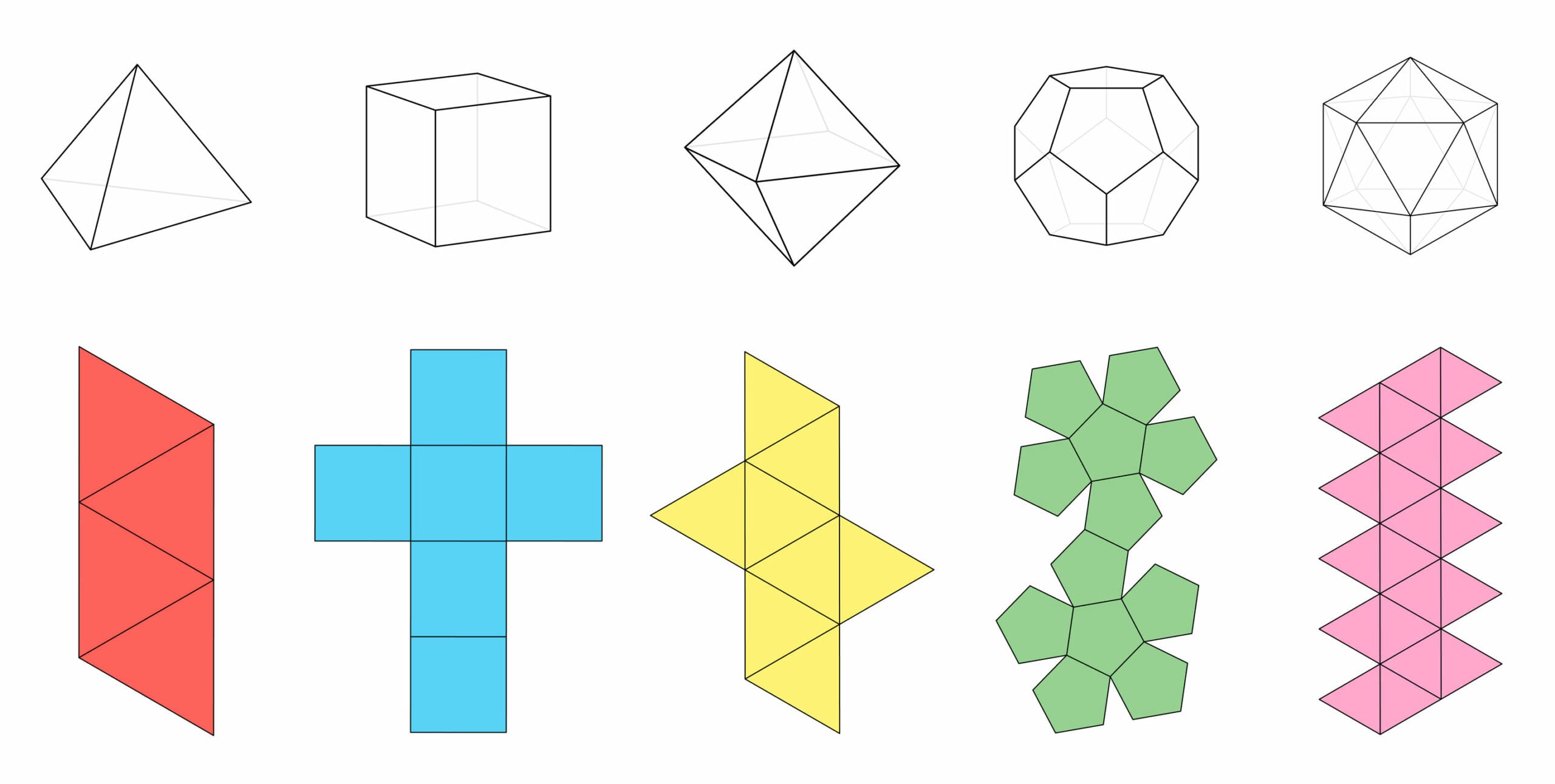
Nets
A net is a pattern of shapes which, when cut out and folded, will become a three-dimensional shape. They are very useful when we want to look at how a surface area is related to a 3D object. Many different nets can be used to make different shapes when cut out and put together.
One of the simplest nets that we will come across is used to make a cube and is shown below.
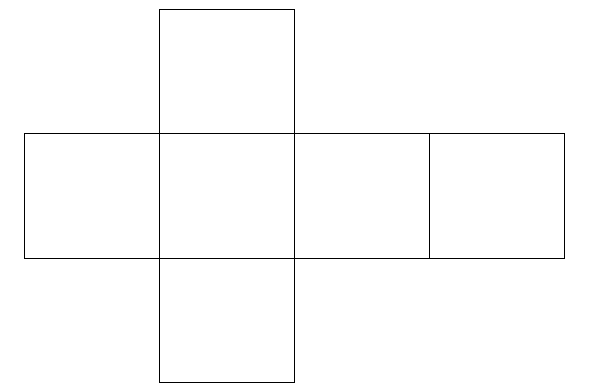
As you can probably tell, when this shape is cut out from the page and folded along the lines it will become a three-dimensional cube.
As already stated, there are many different nets which can be used to make a variety of different 3D objects; some of the more common ones are shown on the next page along with the object which they make.
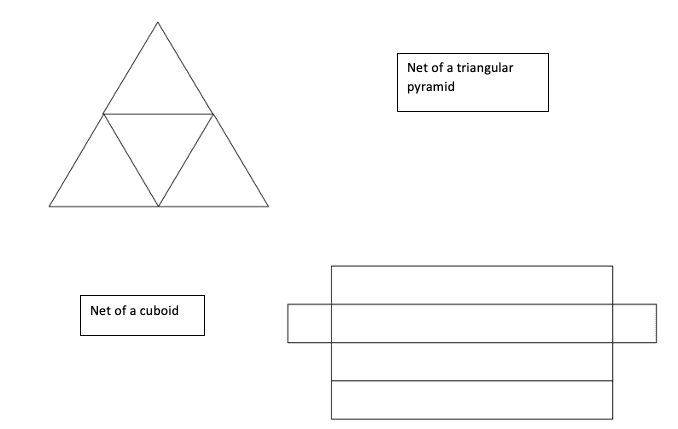
It is perfectly possible to have many different nets for the same shape, as the edges may be folded in different ways.
Surface areas
Using a net of a 3D solid object is very useful if you want to find its surface area. By working out the area of this 2D net we will have the surface area of the entire 3D object which it represents.
If we wanted to find the surface area of a cube of side length 4cm, for example, we can do the following:
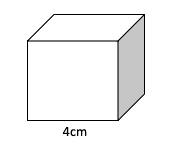
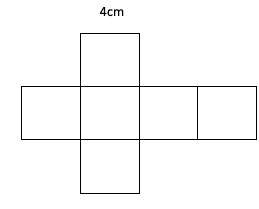
By turning the 3D shape into a net we can easily see that this is made up of 6 squares each of area 
. Therefore, the entire surface area must be 
Obviously, when finding the surface area of a different shape the steps are slightly different, however, as long as you always work out the individual areas of each part and then add these up you will get the correct answer for the surface area.
If we were to work out the surface area of a cylinder, you must work out the area of the middle rectangle in the net and then the areas of both circles on the ends (using area 
), the sum of all these areas is equal to the surface area for the cylinder.
Volume
The volume of a 3D shape is simply the area of the ‘cross section’ of a shape multiplied by its length. The ‘cross section’ is the front of an object like a cuboid or prism. This is shown below.
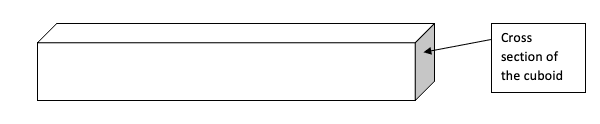
By calculating the area of this cross section we can proceed to multiply this amount by the length of the shape to give us the volume. This is the correct method for any 3D shape when we want to find the volume.
When we worked out areas earlier in the chapter we saw that the units must also be multiplied, leaving us with units that are squared. This is taken one step further with volume as we are now working with three dimensions and the units are multiplied yet again leaving use with units that are cubed. For example, if we had a cuboid with cross section 3cm by 3cm and length 8cm, the area of the cross section would be 
and the volume of the shape would be multiplied by 8cm which is 
. Notice that the units are now in ‘centimetres cubed’ for three dimensions.
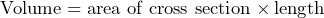
This same rule works for any 3D object, so the volume of a triangular prism and cylinder are as below:
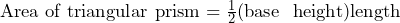
Capacity
The capacity of an object is really the same as volume, however, when we look for a capacity we are really looking to see how much liquid a three-dimensional object can hold. Therefore, the capacity is worked out in the same way as a volume but the units are usually given in something that is more related to liquid such as litres or millilitres. For this reason, it is useful to know the conversions between these units and those that are related to space such as centimetres or metres.
| Spacial units | In shorthand units | Equal liquid units |
|---|---|---|
| 1 cubic metre |  | 1000 litres |
| 1 cubic centimetre |  | 1 millilitre |
From above we can easily see that an object that has a volume of 1 cubic centimetre has a capacity of 1 millilitre, so when we are dealing with any object that has a volume we can easily convert this to a unit that is suitable as a capacity.
We must always remember that the capacity of an object is worked out in exactly the same way as a volume, but just has different units that need to be converted. Therefore, we still must use the formula:
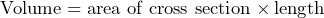
Problems involving Nets and 3D shapes
Many problems can be made using nets, and the techniques that we have learned will come in handy when trying to find the surface areas of shapes in space.
Obviously, when working with such objects, we will need to make use of certain formulae. The two shown below will be given in your examination so you will not have to learn these by heart.
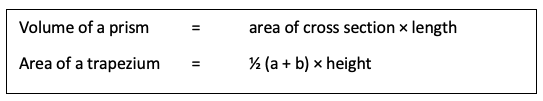
Some of the formulae shown in the next table will be given in your exam, therefore you don’t need to learn these off by heart in time for your test.
Example
A water tank measures 60cm by 20cm by 3m. What is its capacity in litres? Here we use the formula for volume and then convert this into a unit that satisfies the need for a capacity. So we must multiply 60, 20 and 300 (as this is 3m in cm) to give us a volume for the container of 360000
which we now must change using the conversion to millilitres. This then gives us an answer of 360000 millilitres which is equal to 360 litres.
Example
A cylindrical gas container has a cross section which is a circle of radius 40cm and a length of 2 metres. Find the volume of gas which it can hold.
The formula for the volume of a cylinder is 
, so we must put our lengths into this to find the volume. This gives us 
which is equal to 320000
, giving a volume of 1005700.
