In this post
What are formulae?
A formula must have an equals sign and will have one or more unknowns that can take many different values. Because of this, being able to move the parts around to find the different unknowns is very valuable.
Changing the subject of a formula
When we looked at the technique of changing a subject within a formula, or isolating a certain term, we stuck to questions that only had the unknown pop up once in the formula. However, the unknown that we are looking at may occur more than once and we need to know how to deal with this should it happen.
To change the subjects of formulae when the unknown occurs more than once, we need to collect the terms so that they are all on the same side. What we want to do when rearranging any formula for an unknown, say x, is to get a new formula of the type 
, where the right-hand side can be made up of different constants and unknowns but does not contain x. To do this we must obviously bring together all the values of x so that they appear as just one x on the left.
Combining added or subtracted terms
It is rather easy to combine more than one value for an unknown if they are added and subtracted: we must simply move them all to the same side and then do the calculation.
Example
Combine the x terms in the following formula:
To do this we need to move the 
to the left-hand side. We have already looked at how this is done in earlier lessons, where we found out that a sign will change when the subject crosses over from one side of the equals to the other. Therefore, the formula will become:
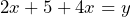
And now the terms can be added to result in just one value of x with a coefficient (in this case 6) in the entire formula.
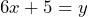
Combining multiplied terms
Sometimes we may see that the terms will have different coefficients, but these can still be combined using the method of factorisation we have already looked at in this module.
Example
Combining the terms of the equation 
can be done by bringing the x value out of the left-hand side to leave 
.
Now we can easily divide both sides by the bracket, which leaves us with:
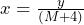
Combining with divided terms
This can be a little trickier, but the same rules for working with formulae and equations still applies for when we move numbers and letters around.
When we have an unknown that we wish to isolate on the top and bottom of the fraction we look to multiply out the bottom and then manipulate the formula in the usual ways to isolate the unknown term.
Example
Suppose we wish to rearrange the following equation for the unknown value y.
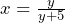
This is a harder problem for us to face but we look to multiply both sides of the equation by the fractions denominator of 
. This will leave us with:
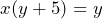
Then expanding the brackets and rearranging terms we see:
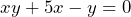
Now we can move the x term to the right-hand side and then use the same technique of factorisation to get just one term of y.
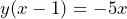
After this we can simply divide both sides of the formula by the bracket and we will be left with just the value of 
Clearly it takes many more steps to rearrange formulae that have the required unknown as the denominator of a fraction, but it is still possible by using a combination of techniques.
To do so we must do the following:
1) Look to multiply out the denominator by multiplying both sides by it.
2) Factorising terms if needed to bring out the wanted unknown value.
3) Adding, subtracting, multiplying and dividing terms where necessary by the techniques that we looked at in module 3 lesson 1.
