Factors and multiples

What are factors and multiples?

A factor is a number that will divide exactly into a given number, leaving a whole number as the answer. For example, 4 is a factor of 20, since  and 2 is then a factor of 4, since .

A multiple on the other hand is a number that can be divided by any number to leave a whole number. It can be made by taking the original number and multiplying by another natural number. So the given number is a factor of the multiple. For example, a multiple of 3 and 5 is 30, since 30 can be divided by both 3 and 5 to give a whole number  and . Therefore, 3 and 5 are factors of 30.

So factors and multiples go hand-in-hand: if A is a factor of B, then B is a multiple of A, e.g. 5 is a factor of 15, and 15 is a multiple of 5.

Note that when we talk of factors and multiples we only ever use the natural numbers (1, 2, 3, …)

Example 1

Find all the factors of 26.

To do this we must try to divide as many numbers into 26 as possible, and it is easiest to start with low numbers.

So 1 obviously divides into any number and is a factor of every natural number. Next we try 2, 3, 4, 5…

We then find that all the numbers that can go into 26 are: 1, 2, 13 and 26 itself, so these are the factors of 26.

Example 2

Find any multiple of 4 and 7.

To do this we must find two numbers which are higher than both 4 and 7 and which, when divided by either, give a whole number.

To do this we need to know that if we multiply two numbers, the result can always by divided by both of the original numbers.

Clearly if we multiply 4 by 7, we get 28, which is obviously a multiple of both 4 and 7.

What is a prime?

A prime number is a whole number which is only possible to make by multiplying itself by 1.

This means that there are no other numbers which you can divide a prime by except for itself (which would divide to get an answer of 1) and 1 (which would divide and give you the same number which you started with, as seen in the last lesson).

Usually prime numbers must be odd, since an even number can be divided by two to get another whole number. The only exception to this is the number 2, which is the first and only even prime number.

The number one is generally not classed as being a prime, so the list of prime numbers goes: 2, 3, 5, 7, 11, 13, 17, 19 and so on.

It will be helpful for you to memorise the prime numbers below 20. There is absolutely no pattern in primes and where they occur. So, for example, they do not crop up after every five numbers or have a certain amount in any group of ten. They appear to turn up at completely random intervals, so it is always a good skill to be able to spot a prime number, and there are certain tricks you can use for this:

• Realising that an even number, apart from 2, can never be prime as it can always be divided by 2 as well as 1 and itself.
• Doing ‘trial and error’ and trying to divide the number by smaller primes, starting with the smallest (this is why it helps to memorise the primes below 20). If a number does not have any factors that are prime numbers, then it must be prime itself.

Example

Is 71 prime?

We can clearly see that 71 is odd, and so cannot be divided by 2, so now we try different numbers that may go into 71.

Starting with 3, then 5, 7, 11, 13, 15 and so on try to divide all the numbers into 71. None of these work, so 71 is prime.

Highest Common Factor (HCF) and Lowest Common Multiple (LCM)

The Highest Common Factor (HCF) is the largest whole number which is a factor of two given numbers. So basically, to find it you have to find all of the factors of the given numbers, as in the previous section, and take the highest one which is a factor of both numbers.

Example

What is the HCF of 18 and 24?

First we find all of the factors of both these numbers. The factors of 18 are: 1, 2, 3, 6, 9, 18 and the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24. So the factors of both of these numbers are the ones which are in both of these lists. Namely: 1, 2, 3 and 6, of which the highest is clearly 6.

So the HCF of 18 and 24 is 6.

The Lowest Common Multiple (LCM) (sometimes called the least common multiple) is the lowest possible number which can be divided by both of the numbers that are given. So if we are given 17 and 9, for example, then the LCM is the lowest possible number which can be divided by both 17 and 9 to give a whole number.

Example

Find the Lowest Common Multiple of 8 and 6.

To do this we must make two lists of multiples: one for each of the numbers given above. So the first few multiples of 8 are: 8, 16, 24, 32, 40, 48… and multiples of 6 are: 6, 12, 18, 24, 30, 36…

Next we can look at the two lists and find the lowest number which appears in both. In this example the number 24 is the lowest, and so the LCM of both 8 and 6 is 24.

It does help save time if you can find the HCF and LCM mentally, however, using the methods explained above can help to avoid miscalculations.

Prime factorisation

To find the prime factors of a number, we must find all the numbers which are factors and are also primes. Any number can be written as a combination of one or more primes.

For example, the prime factors of 24 are 2 and 3, since all of the other factors are not primes. So we can now write 24 as 2×2×2×32×2×2×3 which is equal to 24. So we have broken 24 down into its prime factors.

Expressing numbers as prime factors

All numbers can be broken down into their prime factors. This is where we show a number as a multiplication of only prime numbers, also known as the product of prime factors. To do this we simply find all of the primes that go into our given number and then show these using indices.

Example

Find the product of the prime factors of 40.

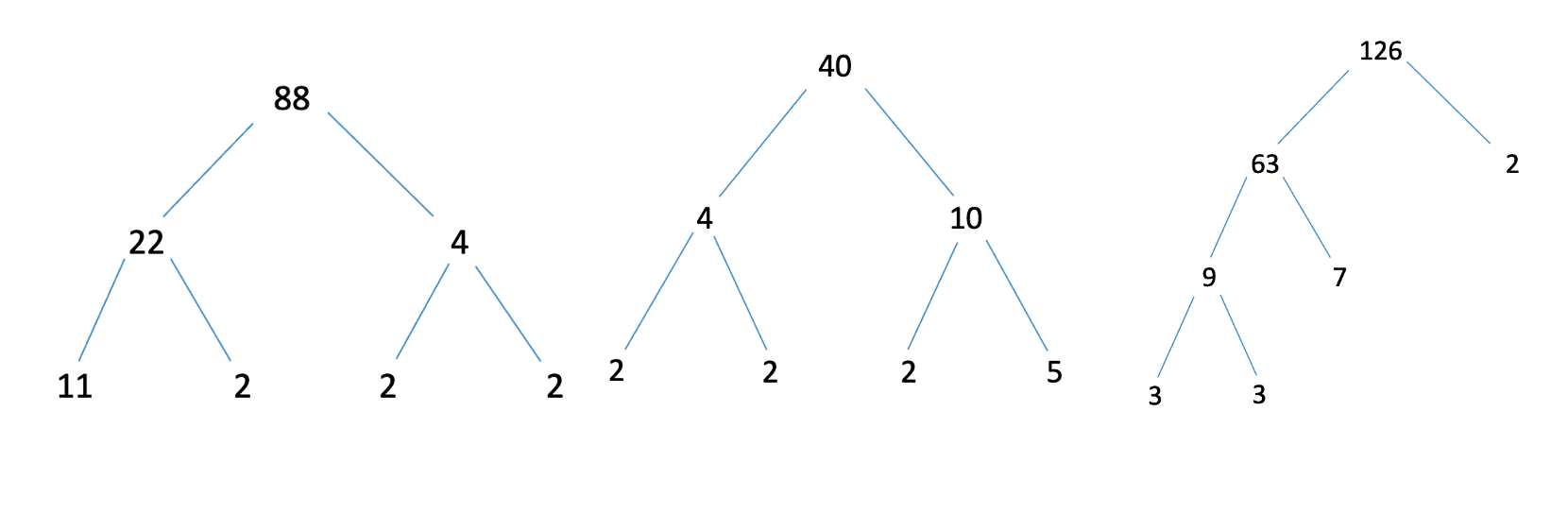
To do this we must split the number into its factors which can be done using a prime factor tree (as shown below). Next we look at the factors that we have and find the factors of these and continue this process. Eventually we will get to the point where we only have factors that are prime numbers.

From the previous diagram we can see that 40 has been split into 4 and 10. Which have then been split down into 2, 2, 2 and 5. These final numbers are all prime so cannot be split down any further. Therefore, we can say that:

40=2×2×2×5=23×540=2×2×2×5=23×5

This method of finding prime factors can be used for any number and allows us to express the number in a very simple form.

Finding the highest common factor

Once we have split a number down into prime factors we can do some interesting comparisons with other numbers. Since the product of prime factors is unique to one number, we can use these to quickly find common factors. For example, if we stick with the number 40 which we now know can be expressed as 23×523×5, and try to find the lowest common multiple of this number and 68, which can be expressed as 22×1722×17, we can use the prime factors to do this:

40=23×540=23×5 and 68=22×1768=22×17

Here we can look only at the prime factors and see that both 40 and 68 have the factor 2 in common. Not only this, they actually share the factor 2222 since the 2323 which is a factor of 40 can be changed to 22×222×2. Therefore, these two numbers share the factor 22=422=4 which is the highest common factor of 40 and 68.

Example

Find the highest common factor of 88 and 126 using a prime factor tree.

So 88=23×1188=23×11

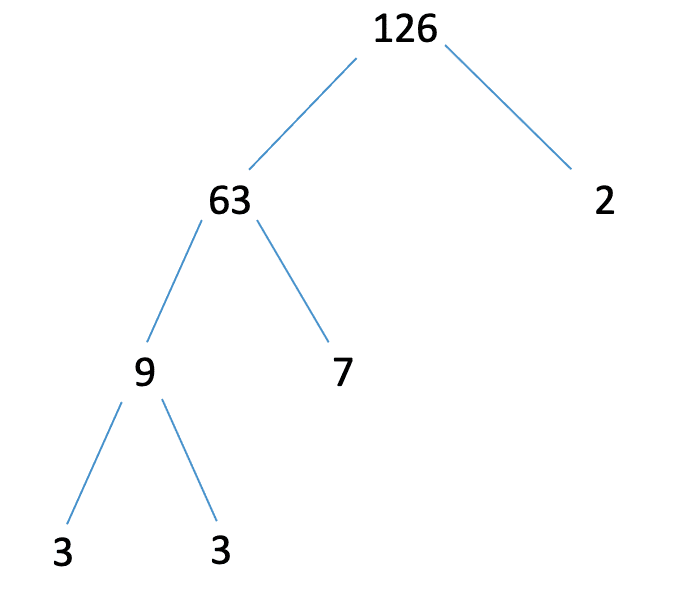
So 126=2×32×7126=2×32×7

Now that we have the numbers as prime factors we can see that 2×33×72×33×7 and 22×1122×11 have 2 as a common factor with no indices so this must be the highest common factor between the two.

Example

Find the highest common factor of 27×32×527×32×5 and 25×3×1125×3×11.

Here we can see that we have 2 and 3 in common so we must investigate both. One of the numbers includes 2727 and the other one has 2525 so we know that 2525 is a common factor since 27=25×2227=25×22. We also have 3 and 3232 so can say that 3 is also a common factor between these two numbers. This means we have both 2525 and 3 as common factors so 25×325×3 is the highest common factor. 25×325×3 is equal to 96.

Finding the lowest common multiple

After splitting two numbers into their prime factors we can also find the lowest common multiple. In order to do this we must first get the highest common factor using the approach that we have just worked through. We need to also know the prime factors of the two numbers. Once we have these, we can follow the steps below to find the LCM:

1) Find the HCF.

2) Find the prime factors and cancel out any common factors.

3) Multiply the HCF by the remaining prime factors.

Example

Find the lowest common multiple of 27×32×527×32×5 and 25×3×1125×3×11.

1) In this example we are using the same numbers as previously where we found the HCF to be 96.

2) We now need to cancel out any common factors from 27×32×527×32×5 and 25×3×1125×3×11:

2×2×2×2×2×2×2×3×3×52×2×2×2×2×2×2×3×3×5

2×2×2×2×2×3×112×2×2×2×2×3×11

Cancelling out the common factors leaves us with:

2×2×3×5×112×2×3×5×11

3) Multiplying the numbers from parts 1 and 2 gives us 96×2×2×3×5×11=6336096×2×2×3×5×11=63360 as the lowest common multiple.