Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the autocomplete-woocommerce-orders domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114

Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the edwiser-bridge domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114

Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the wc_bulk_discount domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114

Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the affiliatewp-affiliate-portal domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114

Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the affiliate-wp domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114

Notice: Function _load_textdomain_just_in_time was called incorrectly. Translation loading for the woocommerce domain was triggered too early. This is usually an indicator for some code in the plugin or theme running too early. Translations should be loaded at the init action or later. Please see Debugging in WordPress for more information. (This message was added in version 6.7.0.) in /www/onlinelearningcollege_157/public/wp-includes/functions.php on line 6114
Mastering Fractions: Key Rules For Division And Multiplication

Dealing with fractions

April 25, 2022

Dividing and multiplying fractions

In this post

We have already looked at multiplying and dividing fractions earlier and the exact same methods and principles are used even when we have unknowns in the fraction. We will recap these first.\

\frac{2}{3} \times\frac{1}{4} =\frac{2 \times 1 }{3 \times 4 }=\frac{2}{12}

\frac{3}{4} \div \frac{5}{3} =\frac{3}{4} \times \frac{3}{5} =\frac{3 \times3 }{4 \times 5 }=\frac{9}{20}

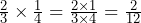
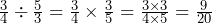
From these easy calculations we can form a rule that is used for all calculations when multiplying or dividing fractions:

Dividing and multiplying fractions

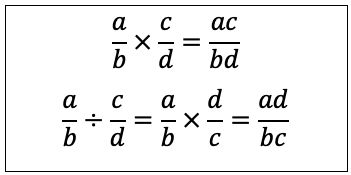
From these formulae we can easily manipulate formulae that involve multiplication and division of unknown values in fractions: we need to just stick to the formulae outlined above.

One thing which we will need to look into, however, is simplifying the fraction once the calculation has been done. Suppose we have the equation $\frac{ac}{bc}$ , we can clearly cancel the unknown variable c which appears on the top and bottom of the fraction. This can be done because of the following reasoning:

\frac{ac}{bc}=\frac{a}{b} \times\frac{c}{c}=\frac{a}{b} \times 1 =\frac{a}{b}

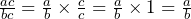
So, for any fraction we must always look for different unknown values that we can cancel from the top and bottom to make sure that the fraction is in its simplest form.

Example

Simplify the following:

\frac{2xy}{z} \times \frac{zx}{y^2} \div\frac{z}{xy}

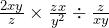
First, we must do the multiplications and division shown here then we can think about simplifying the result. Doing the multiplication first we get

\frac{2xyzx}{zy^2} \div \frac{z}{xy} = \frac{2x^2yz}{zy^2} \div \frac{z}{xy}

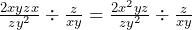
Next, we can swap the end fraction and convert the division into a multiplication which results in:

\frac{2x^2yz}{zy^2} \div \frac{z}{xy} = \frac{2x^2yz}{zy^2} \times\frac{xy}{z}=\frac{2x^3y^2z}{z^2y^2}

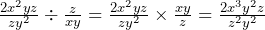
Now all that is left for us to do is simplify the fraction by cancelling any common terms from the top and bottom. The common terms are $Dealing with fractions$ and z:

\frac{2x^3y^2z}{z^2y^2}=\frac{2x^3}{z}

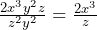
So now the equation that we started with has been calculated and put into its simplest possible form by cancelling any common unknown values.

Looking to get a GCSE?

We offer a wide range of GCSE courses.

Start your learning journey

Speak to a friendly course advisor to learn more about the best qualification for you.

Speak to an advisor

Read our policies