Different regular polygons can be made from circles by equally dividing them into the correct number of segments. To do this we need to know the number of sides that the polygon has and use this to draw in the correct number of lines that cut the circles. Then these can be connected to give us the regular polygon required.
Steps:
1) Find the number of sides in the polygon that we are trying to draw, e.g. an octagon has 8 sides, hexagon has 6 etc.
2) We then need to divide the degrees in a circle, 360, by the amount of sides that we need.
3) Next draw a line through the centre of the circle splitting it into two.
4) Draw another line that is the number of degrees found in step 2 around from the line drawn in the previous step.
5) Use this new line to repeat step 4 and continue until we have drawn lines all around the inside of the circle.
6) Connect all of the edges of the drawn lines and then carefully erase the original circle.
Example
Draw a regular octagon using the method outlined above.
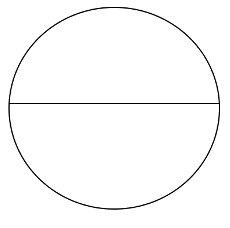
Carrying out the correct steps we begin with drawing a circle and simply draw a line through the centre:
Next, we divide the \( 360^\circ \) in a circle by the number of sides in an octagon which gives us \( 45^\circ \). Therefore, we need to draw another line which is from the one we have already drawn.
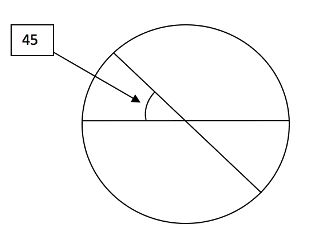
Then, by continuing to draw new lines that are each 45° away from the previous, we form the following:
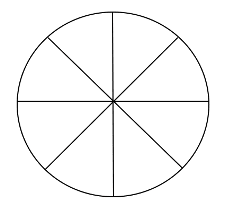
Then we join up the edges of the lines to the next:
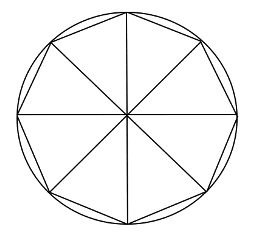
Then by erasing the original circle and the lines which intersect it we have drawn a perfect octagon with all the sides and angles equal.
This trick can be done for any different regular polygon by simply finding the correct angle by dividing \( 360^\circ \) by the correct number of sides for the shape needed.
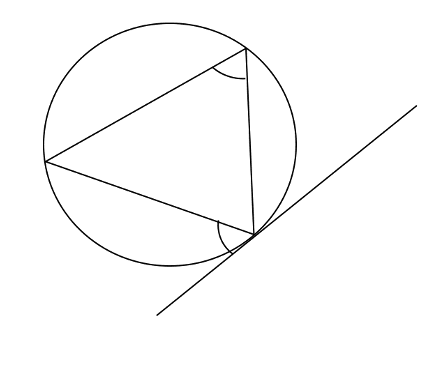
The alternate segment theorem
One last theorem which you must know, again involves circles and tangents. If we draw a circle with a tangent and then form a triangle within the circle with one vertex touching the same point as the tangent, then we find some equal angles. This is shown in the diagram below:
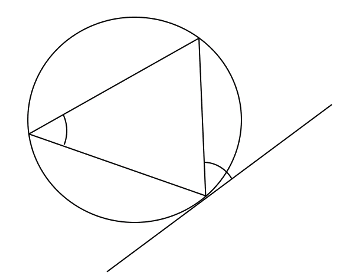
The two angles shown will be equal to one another in this case and the other angles shown below will be also: