Bearings

April 7, 2022

In this post

Bearings are used for navigation purposes mainly, however, you will need a good understanding of them for this course. They use angles around a circle as a way of locating objects from a fixed point. If we look at a traditional compass, like below, we see that the points North, East, South and West are at 90 degree angles from each other.

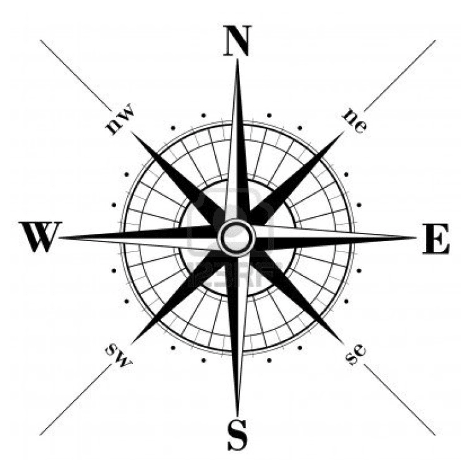
This can be extended to show different points that are between the main four of a compass. In reality we could be anywhere in the circle and would define the position using an angle from the North line.

Rules for bearings

Always measure your angle from the North line; this is classed as a basic point of reference in any problem.
Be sure to measure correctly when clockwise or anticlockwise measurements are needed. Bearings will always be in the clockwise direction unless stated otherwise and the angles should always be done in this direction.
If your angle has only 2 digits, say 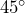$45^\circ$ , this should be written with a zero, as 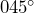$045^\circ$ . This is so all angles have 3 digits to avoid any mistakes.

If we wish to plot a point that is a certain distance from another using a bearing, we must first draw a North line from the start point. Then an angle must be stated for the next point, which is always in the clockwise direction (unless otherwise stated). And finally, a distance should be given to get to the end point.

Finding the angle

From the start point a North line is drawn. We then must measure the angle that is stated in the clockwise direction. Next, the angle must be drawn and the end point is then somewhere on this line.

Above shows a $045^\circ$ angle in a clockwise and an anticlockwise orientation. If you come across a question that is for bearings, you must assume the rotation is clockwise. The angle is then measured in the correct direction from the North line that we have put in. A distance between the start and end points should then be given so that the end point can be located exactly.

Going back to the start point

When we have found a way to get from one point to another we may then need directions to get back to where we started from. To do this we must draw a North line from the second point and then figure out the method needed to get back to the original point.

From the example we had on the previous page, where we had an end point that was $045^\circ$ clockwise from the original, to get back to the start point we must rotate by $225^\circ$ clockwise. The distance between the two points will be the exact same as before, but the angle is changed so that it is $180^\circ$ more than the original and still in the clockwise direction.

This is not always the case for bearings. Therefore, to get back to the original point we must draw a new diagram that has the second point as the start. We can then put in the original angle that we had and work out the bearing that we need through the use of alternate angles.

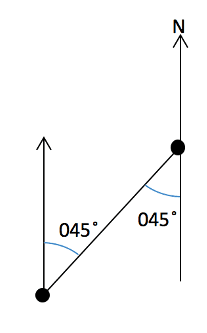
Using alternate angles we can find the opposing angle in the diagram that is also $045^\circ$ . This is then used to solve for the angle that we need, which in this case is equal to $180^\circ+045^\circ$ giving an answer of $225^\circ$ .

Example

A point B is South-West of a point A. Find the bearing of:

a) B from A

b) A from B

a) We must start from the point A and find a clockwise angle to get to B. This is shown in the diagram below

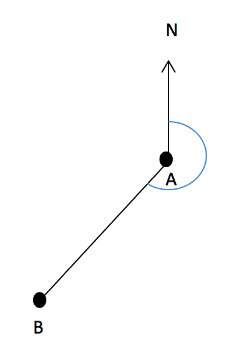
Since we know that B is South-West of A we know that the angle is five eighths of the way around a full circle. Therefore, the angle A must be $225^\circ$ .

b) Getting from the point B back to A is a little trickier as we need to reverse the use of the original bearing. Again, we should draw a diagram but this time have the origin as the point B and the North line here.

By extending the two vertical lines and putting in the angle of $225^\circ$ which we already know, the problem becomes one where we need to find an unknown angle with parallel lines. We already know how to do this and using the idea that alternate angles are equal and angles on a straight line add up to $180^\circ$ we can find the unknown angle x.

The angle which is $225^\circ$ is made of two parts, one that is a straight line so is $180^\circ$ and another which is an alternate angle to the one which we want to find, x. Therefore, if we split the angle into two we can find the unknown angle fairly easily.

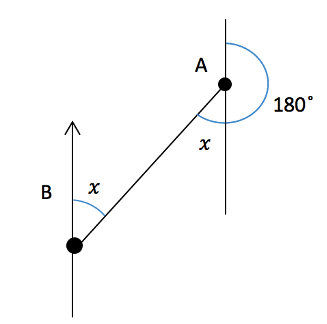
The angle must therefore be equal to $225^\circ-180^\circ$ which is $045^\circ$ . So the bearing from B to A is $045^\circ$ .

Drawing bearings problems

One of the main things that you must master when dealing with bearings is to be able to draw the problem and the angles that are given. By plotting the points that are mentioned we can change a worded problem into one dealing with simple angles that we have already learned to solve earlier in this chapter. A question will always have a start point, say A, and another point which will be at a certain angle to this. It is much easier to draw these in immediately, but do not worry about accuracy when doing this as we only need a sketch. However, make sure the angles are roughly the right size to avoid confusion, so do not draw an acute angle as reflex in your diagram for example. When drawing, start with the initial point and then move round from the North line the correct amount of degrees and then plot the second point and mark down the angle, then any lines can be extended and, through the use of opposite angles, corresponding angles and angles on a line, we can work out any unknowns.