In this post
A tangent is something which we have already looked at and involves a straight line which just touches a curve or shape in one place but does not actually intersect any side of the shape.
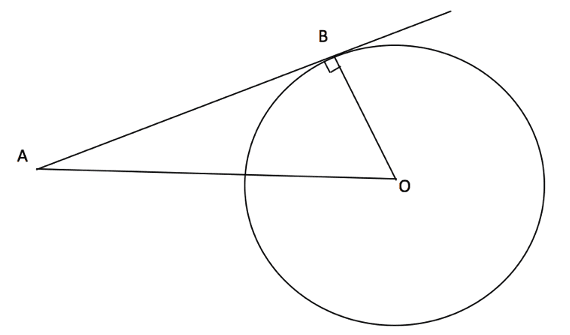
Theorem 1
A tangent to a circle will always be at a right angle to the radius.

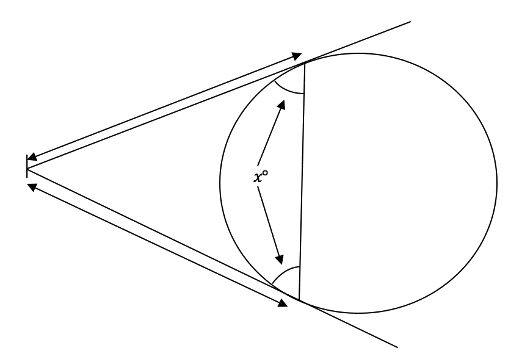
Theorem 2
Tangents to a circle from the same point are equal in length
Drawing two tangents from the same point outside a circle will make the two lines exactly equal to one another, as shown above.
This theorem can also be extended to say that the two points where the tangents meet the edge of the circle can be connected and this will create an isosceles triangle since the two tangent lines are equal in length.
Example
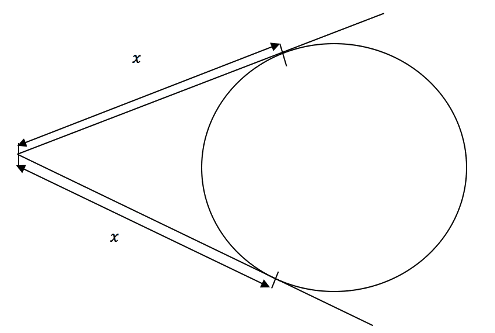
Find the length of AB in the following if the circle’s radius is 5m and AO is 15m:
We simply have a right-angled triangle so ![]() so
so ![]()
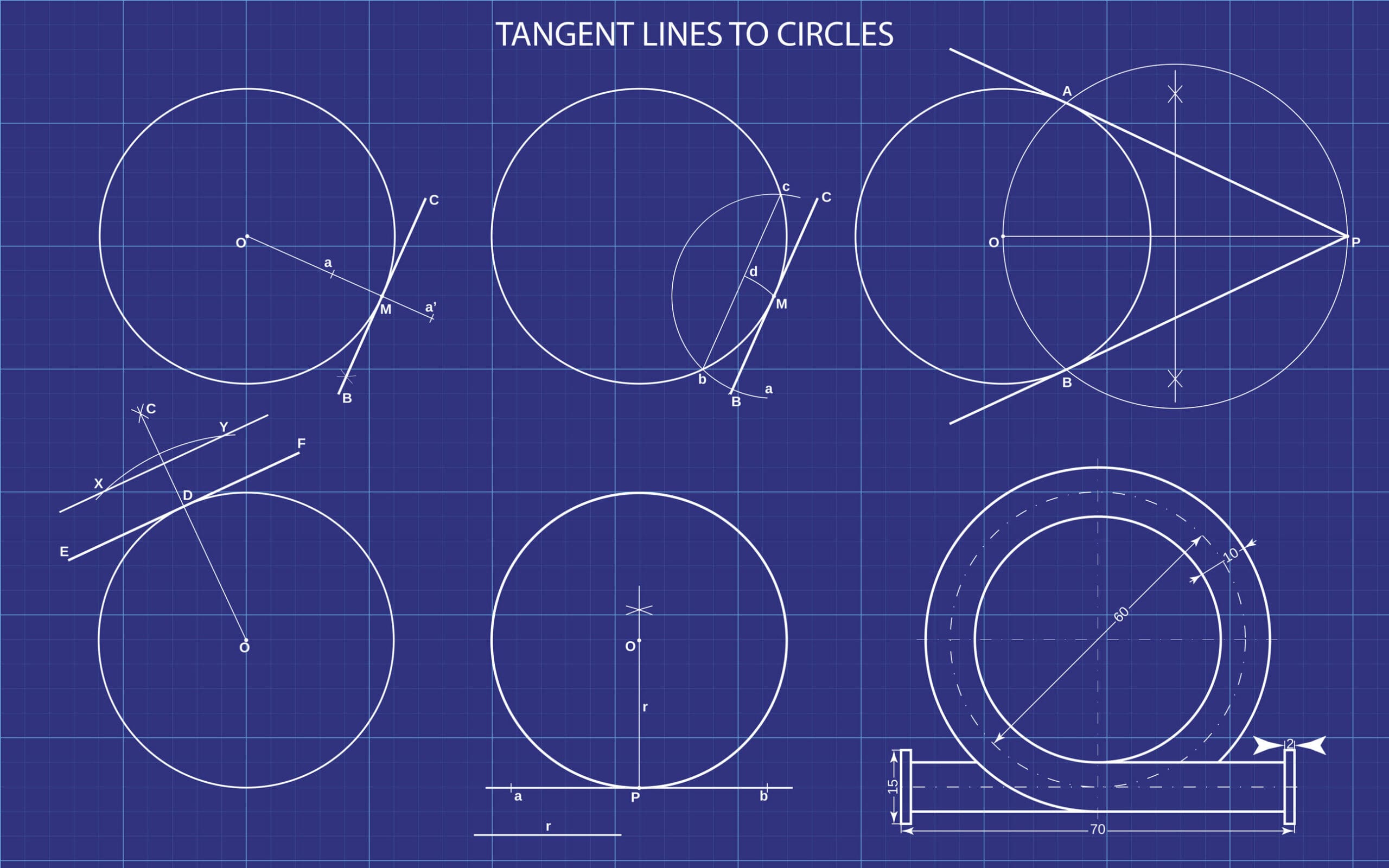
Example
Find the size of the angle x where the two lines are tangents to the circle.
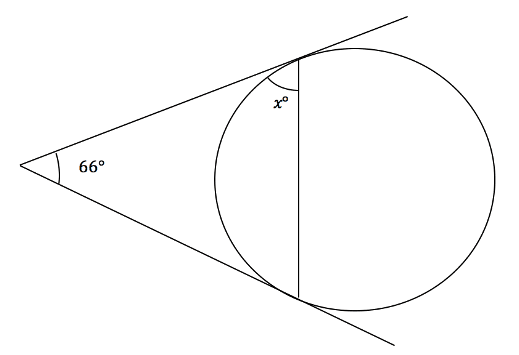
Since the lines are tangents, the angle to the other side of the circle connecting the other tangent must also be equal to ![]() . This means that we have a triangle with one angle
. This means that we have a triangle with one angle ![]() and the other two both equal to
and the other two both equal to ![]() . Since angles in a triangle must add to
. Since angles in a triangle must add to ![]() then the value of must be
then the value of must be ![]() .
.