In this post
An irrational number is one which cannot be expressed as a definite decimal as it continues on forever. For example, the square root of 3 (which is ![]() ) is irrational as the answer is 1.73205… and will continue on forever.
) is irrational as the answer is 1.73205… and will continue on forever.
A surd is an irrational number that contains a square root. This can be at the top or bottom of a fraction, multiplied by something or added/subtracted from another number. Some examples of surds are:

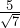

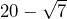
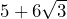
Simplifying surds
When we have two surds that are multiplied by one another we can use a technique to simplify them so that instead of having two things multiplied by each other we can gather the terms and then put them under the same square root. This is done by simply multiplying the two numbers in the square root and then putting this as a square root. For example:
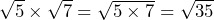
Using the same reasoning, we could separate a surd into two by finding the two components that will multiply together to give the larger. This can then help us to simplify the surd and bring out some whole numbers. For example:

By realising that 80 is the same as 16 times by 5 we can separate the surd and then see that ![]() is equal to 4 and so the whole thing is then the same as
is equal to 4 and so the whole thing is then the same as ![]() .
.
When we are given a surd we may be asked to express it in its simplest possible form. This basically means that we must simplify it so that we have a whole number on the outside and the number in the square root cannot be simplified any further by this method.
Example
Simplify the surd ![]() .
.
By looking for square numbers that are factors of 108 we can separate the number into different surds to simplify. 4 is a square number that will go into 108. So we can spilt the surd:
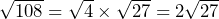
Now we have the surd ![]() which can also be simplified! The square number 9 is a factor of 27 so this can be separated out.
which can also be simplified! The square number 9 is a factor of 27 so this can be separated out.
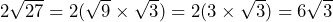
So we have now found that the surd ![]() can be simplified to
can be simplified to ![]() .
.
Rationalising the denominator
We have already looked at how to rationalise the denominator of a fraction in an earlier lesson, however, it is a bit different when we are looking to rationalise a surd that is a denominator.
When rationalising a surd we need to find a way to simplify something that may look like ![]() . The way in which we do this is to multiply the top and bottom by the surd that is the denominator (remember that a number with equal numerator and denominator is 1 and that multiplying by 1 does nothing to a number). This will then square the surd at the bottom and therefore will leave us with a whole number as the denominator.
. The way in which we do this is to multiply the top and bottom by the surd that is the denominator (remember that a number with equal numerator and denominator is 1 and that multiplying by 1 does nothing to a number). This will then square the surd at the bottom and therefore will leave us with a whole number as the denominator.
So in this case:
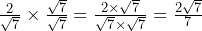
We have managed to get rid of the square root that is on the bottom of the fraction and replace it with one on the top. This makes the number much more manageable when we look to do other things as we do not have a square root on the bottom of the fraction.



